Euler Characteristic Exploration

Objective: Compute the Euler characteristic for some polyhedra and some other surfaces.

In 1750, the Swiss mathematician Leonhard Euler noticed a remarkable formula involving the number of faces F, edges E, and vertices V of a polyhedron. It is now called the Euler characteristic, and is written with the Greek letter $\chi$:

The Euler characteristic is $\chi$ = V - E + F

For the Platonic solids, the Euler characteristic is always 2.

Polyhedra

The Euler characteristic of a shape is the value of V - E + F and is usually written as $\chi =V-E+F$.

1. Escher's Ivory Ball Study shows a Rhombic dodecahedron, with twelve rhombic faces. Compute V, E, F and $\chi$ for this polyhedron.
2. The dual of the Rhombic dodecahedron is the Cuboctahedron, which is a cube with its corners cut off, or equivalently, an octahedron with its corners cut off.
   Compute V, E, F, and $\chi$ for the Cuboctahedron.
3. Compute V, E, F and $\chi$ for the tessellation by 45°-60°-90° triangles in Concentric Rinds.
4. Compute V, E, F and $\chi$ for the Deltoidal Icositetrahedron.

Cuboctahedron as a spherical tessellation

Deltoidal icositetrahedron as a spherical tessellation.

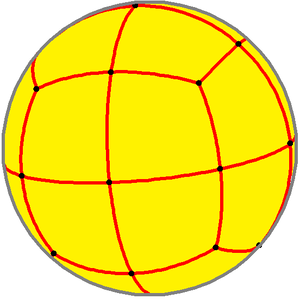
The Euler characteristic of a Polyhedron is always 2.

Surfaces

Here, you will compute the Euler characteristic of tessellations that are not on the sphere:

5. Compute V, E, F and $\chi$ for this square lattice:
6. Compute V, E, F and $\chi$ for this graph:
7. Compute V, E, F and $\chi$ for this picture of a torus:

Handin: A sheet with answers to all questions.