Fractal Dimension Exploration

Objective: Finding the dimension of fractals.

We can compute the dimension of an object by dividing the sides into r segments (more precisely: the linear scaling factor is r), and counting the number of replacement segments N we obtain:

$Dimension={\frac {logN}{log(r)}}$

(For information on how to use the built-in Calculator on a Mac, see below.)

For example: Take a square, and divide all sides in two (so r = 2). This gives us four smaller squares (so N = 4).

Then we obtain: $Dimension={\frac {log4}{log2}}=2$ . This is no great surprise of course, but this (strange) formula will help us compute the dimensions of self similar fractals.

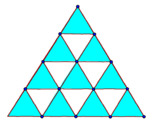
Suppose we take a triangle and divide all sides in fourths (r = 4: r measures the scaling of lines) and we keep 10 of the small triangles (N = 10). (There are 16 small triangles, but we keep only 10 of them.) We obtain: $Dimension={\frac {log10}{log4}}=1.66$

This means that if we repeat the process (i.e. divide each small triangle into 16 smaller ones and keep only 10 of those), then the resulting shape has dimension 1.66.

A fractals is an objects whose dimension is not a whole number, hence the name fractal.

1. The Sierpinski Triangle:

a. What is r (scaling ratio)?

b. What is N (number of pieces we keep)?

c. Calculate the dimension.

2. The Koch Edge

a. What is r (scaling ratio)?

b. What is N (number of pieces we keep)?

c. Calculate the dimension.

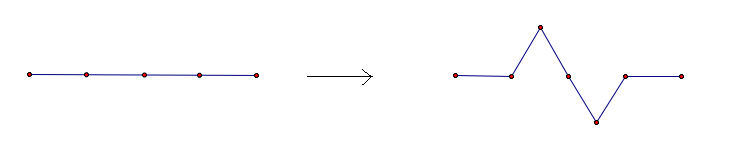
3. The Zig-Zag curve. We divide a line segment into four congruent parts. Replace the two segments next to the middle by two new segments as indicated.

a. Draw one more iteration of the Zig-Zag curve.

b. What is r (scaling ratio)?

c. What is N (number of pieces we keep)?

d. Calculate the dimension

---

Here's how to use the Calculator on a Mac to evaluate the expressions in this Exploration:

First go to the Applications folder (which you can see from the Dock) and open Calculator.

Next, under the View drop-down menu, select Scientific (in older Macs, this is Advanced) and Show Paper Tape (i.e., View > Scientific and View > Show Paper Tape).

To calculate, say, log(5)/log(3), hit the keys on the Calculator in this order:

• 5
• log
• divide-key
• 3
• log
• =

The Calculator will show the intermediate results of log(5) and log(3), without showing what's going on; but the Paper Tape will make it all clear.

Then to do another calculation of the same form, just edit the Paper Tape. For instance, to find log(5)/log(2), change the 3 on the Pape Tape to 2, and then hit the Recalculate Totals button on the Paper Tape.

Handin: A sheet with answers to all questions.