Instructor:Polygonal Tessellation Exercises Solutions

Polygonal Tessellation Exercises

1. Geometric tessellations: Squares – squares and rhombi – another squares and rhombi – squares – hexagons – triangles – rhombi – squares. (The purpose of the question is to tie in the work of MC Escher again. Students should give good descriptions. They should be able to communicate what they know and observe in complete sentences.)
2. The print “Verbum” is based on a triangular tessellation. Escher used this tessellation to create a picture where shapes morph into other shapes. The fish (land) morph into frogs (land), which in turn morph into birds (air). There is also a duality between black and white animals. The common theme of the three prints is that all depict earth, water, and air in a single scene. (This is not a purely mathematical question. The purpose is to see if students can recognize patterns. In this case the patterns involve the animal shapes morphing from one animal into another.)
3. The tessellation should contain at least 12 triangles and should show a pattern. The easiest way to create the tessellation is to rotate about the midpoints of the side. Examples:
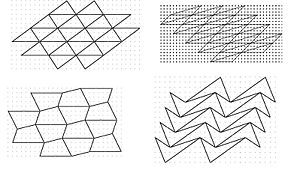
4. a) A, C, D are convex. b) A, C, E can tile.
5. sketch: One possibility for students is to just trace one of these tessellations from page 225, 226 or 227. Note that the discussion and drawing on page 106 would allow them to copy the pattern on grid paper.
6. There are many possibilities, but the rhombus (sides are congruent, angles are not) and a rectangle (angles are congruent) are the easiest examples.
7. The angle sum is (11-2)180 = 1620. The measure of one angle is 1620/11=147.27 (rounded off to 2 dec. pts.)
8. This question asks the students to summarize the lab called “why there are only three regular tessellations”. The answer should include a description of all the steps involved.
9. octagons and squares
10. hexagons and triangles
11. A quick computation shows that the regular pentagon has an interior angle of 108 degrees, and a regular decagon has an interior angle measure of 144 degrees. 108+108+144 = 360. Hence 2 pentagons and one decagon will fit exactly at a vertex. Note that we will run into problems when we try to extend this tessellation across the plane. (One problem is indicated by a circle.)
12. The 9-gon has corner angles 140 degrees. An 18-gon would fit in the gap.
13. Tetrominoes. There are many different tessellations. The students need to establish some pattern that shows they have created a periodic tessellation. Here are some examples:
14. Pentominoes: The ‘+’ only tessellates in one way. Remember that the tessellation needs to show a pattern. Ad hoc, partial tessellations of the plane should not receive credit. I.e. a pattern should be evident in the tessellation.
15. Of the 108 septominos, only four cannot tessellate, and these are shown below. Students should probably find the first one, with the hole, which is often considered to be 'not a septomino' in mathematical literature. See Grünbaum-Shephard, Tilings and Patterns, 1987, page 502 for details.
    
16. It depends a bit on how one looks at it: I. This tessellation can be thought of as being made up from squares and rhombi. Looked at in this way, the tessellation is neither regular nor semi-regular. (a rhombus is NOT a regular polygon). II. The tessellation can also be thought of as made up of triangles and squares. In this case the vertex configuration is (4,3,3,4,3) everywhere. And this is indeed one of the semi-regular tessellations.
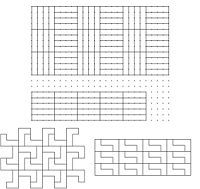
17. Mondriaan: Both tessellations are made up from rectangles and squares. There is no repeating pattern, hence the tessellations are aperiodic. (There’s no translation that maps the tessellations to itself.)
18. Kandinsky