Knot Theory

Relevant examples from Escher's work:
Introduction
Knots have been used in decorations for centuries. Ornamental knotwork borders were used by the Egyptians, Greeks, Romans and many other civilizations.


The examples of knotted borders from staffs belonging to the Pharaoh Tutankhamen (ca.1340 BCE) show how far back in time these types of decoration were used. These borders are not much different than some found on a highland dirk handle, Byzantine borders, etc. G. Bain[1] mentions that some of the earliest knotted or plaited borders may have been an imitation of patterns observed in weaving and basketry.
Celtic and Nordic Art
Knotted figures appear in Celtic and Nordic art and these images date back at least two thousand years. Sometimes they created intricately knotted figures of varying shapes, and at other times the knotted figures were combined with animals. One might find for instance a lion with its body made of of some intricately knotted figure.
Zoomorphic knots from the Cathedral Basilica in St. Louis:

|

|
One can think of a knot as a string that is knotted up, and then has the ends tied together to prevent it from becoming undone. Mathematically we would say that a knot is an embedding of the circle in 3-space.


The knot as an unending loop which is twisted up is sometimes seen as a symbol of the infinite. In Ireland the Celtic crosses are often shown as intricate knotted figures. These Celtic crosses are a combination of some pagan imagery and Christian beliefs. The Irish believed that the Celtic cross was brought to Ireland by Saint Patrick. The intricate knot work was also used to decorate the gospels of the day, and the monks produces for instance the Lindisfarne gospels, the Book of Kells, the Echternach gospels, etc. The knot was seen as a symbol of infinity and as a symbol of continuity. G. Bain mentions that in constructing some of the intricate knots the artists knew which methods of construction would result in one connected line - a knot- and which constructions would result in a pattern consisting of two or more seperate lines woven together. If the interlaced pattern consists of two or more components, then mathematically this is called a link.
In the 19th century the interest in knots saw a resurgence. Lord Kelvin, a British scientist, conjectured that atoms were knotted vortices in the ether. The idea was that the universe was filled with ether (an invisible fluid) and that the building blocks of the molecules could be thought of as knots in this ether. Scientists attempted to create tables of knots depending on how many crossings there were in a drawing (diagram) of the knot. This resulted in the first known knot tables. The theory of Kelvin was later replaced by other theories about the nature of our basic matter and the theory of knots was put on the shelf.
In the latter part of the 20th century there was a renewed interest in knot theory. Strands of DNA can sometimes form knots, and some mathematical techniques that play a role in quantum mechanics are related to knot theory for instance.
Knot Tables
In the 19th century Tait, Kirkman and Little started tabulating the knots in so called knot tables. The knots are listed in order grouped by the number of crossings. Below you see a copy of the knot table for knots with 3 to 7 crossings.
The knot in the top left corner is special. It is often called the unknot. It is a simple circle with no knotting. As you see there is exactly one knot with 3 crossongs. This knot is often called the trefoil knot. There is also a unique knot with four crossings: the figure-eight-knot. In some pictures part of the knot will resemble a figure eight.
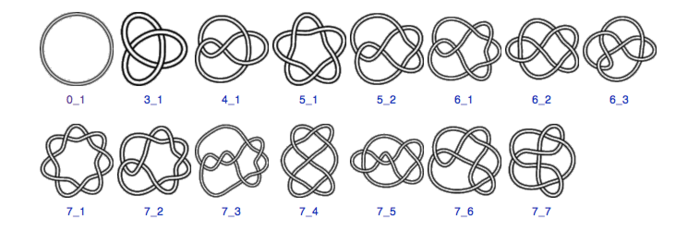
The original image can be found at The knot Atlas page.[2]. On this site you can click on the knots to obtain more information.
An important question is: Can we recognize the unknot?
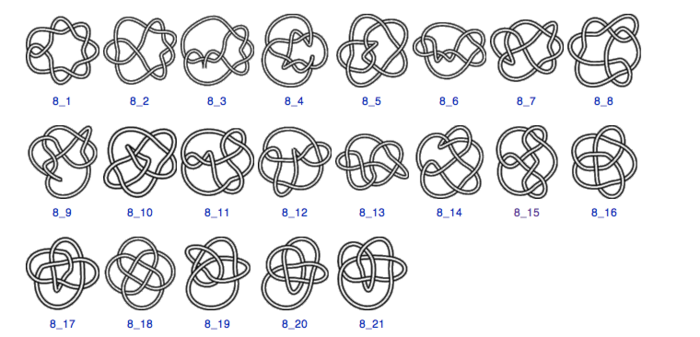
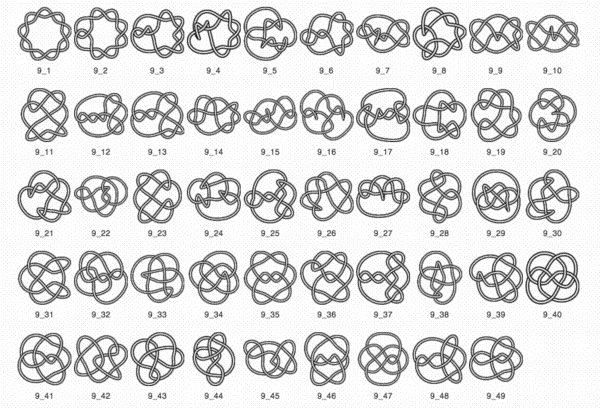
Related Sites
Notes
- ↑ Bain, George, Celtic Art: The Methods of Construction, Dover (1973) ISBN 0-486-22923-8
- ↑ http://katlas.math.toronto.edu/wiki/The_Rolfsen_Knot_Table The Knot atlas