Regular Triangle Symmetry Group Exploration

Objective: Understanding the finite symmetry groups.

The square

Complete the multiplication table for D4, the symmetry group of the square.

	$E$ (identity)	$R$ (rotation 90)	$R^{2}$ (rotation 180)	$R^{3}$ (rotation 270)	$M1$ (reflection)	$M2$ (reflection)	$M3$ (reflection)	$M4$ (reflection)
$E$
$R$
$R^{2}$
$R^{3}$
$M1$
$M2$
$M3$
$M4$

The equilateral triangle

Analyze the symmetry group D3 of the equilateral triangle:

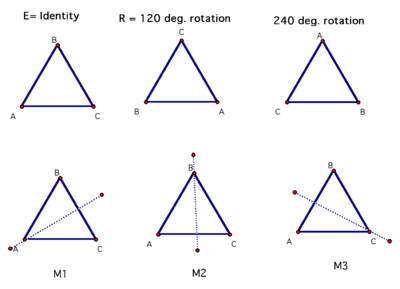
1. How many elements are in this group?
2. What is $M1$ x $M1$ = $M1^{2}$? , $M2$ x $M2$ = $M2^{2}$? , $M3$ x $M3$ = $M3^{2}$?
3. What is $M1$ x $M2$? , $M2$ x $M1$? , $M3$ x $M1$? , $M1$ x $M3$? , $M3$ x $M2$? , $M2$ x $M3$?
4. How do rotations behave?
5. Can you spot C3 as a subgroup of D3? What is it?
6. Find all subgroups.
7. Write out a multiplication table for D3.

Handin: A sheet with answers to all questions.