Tessellation Exploration: The Basics

Objective: Find a method to tessellate the plane with any triangle. Introduce regular and semi-regular tessellations.

Materials

• Printed copy of the Tessellation Exploration: The Basics.

Tessellations by Triangles and Quadrilaterals

1. Convince yourself that the parallelogram below will tessellate the plane. Draw your tessellation on a separate piece of paper. It should cover 1/4 of your page.

   

2. Show that a square tessellates the plane and show that a rectangle tessellates the plane. Your tessellations should cover 1/4 of your page.
3. Draw an acute, an obtuse and a right triangle. Now convince yourself of the fact that two congruent copies of the same triangle fit together to form a parallelogram or a rectangle.
4. Why does this imply that all triangles will tessellate the plane?

Tessellations of the Plane by Regular Polygons

A regular tessellation is a tessellation made of regular polygons, all congruent to one another. (Recall that a regular polygon has all sides congruent to one another and all angles congruent to one another. This implies the polygon is convex--why?)

A semi-regular tessellation is a tessellation made of regular polygons of two or more types so that the arrangement of polygons at each vertex is the same.

5. What is the common name for a regular 3-gon?
6. What is the common name for a regular 4-gon?

A tessellation is a regular tessellation if it is constructed from regular convex polygons of one size and one shape. There are exactly three regular polygons that tessellate the plane: the equilateral triangle, the square, and the regular hexagon.

Note for instance that the regular pentagon does not tessellate the plane! The figure below shows that when we try to arrange the pentagons around a vertex, then we will always have a gap or an overlap.

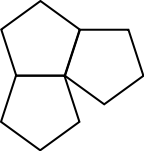
There are non-regular pentagons that tessellate the plane.

7. Sketch the tessellation for a pentagon that looks like the outline of a house (see below) to illustrate this point.

   

Semi-Regular Tessellations

We can also look at tessellations formed by a combination of several regular polygons. A tessellation is a semi-regular tessellation if it is composed of regular polygons of two or more types so that the arrangement of polygons at all the vertices is the same.

8. Extend the following tessellation. You should draw at least 2 more layers of polygons on each side. Is this tessellation semi-regular? Explain.

   

9. Are the following two tessellations semi-regular or not? Explain.

   

Handin: A sheet with answers to all questions.