Random Tessellation Exploration

Objective: Produce tilings using randomized methods

Materials

• Graph paper
• Domino rotation grid

Procedure

1. Using a piece of graph paper, make a 5x5 grid of squares, each one of which contains four graph paper squares. For each big square, flip a coin and use the result to divide into two dominoes either horizontally or vertically. Continue until you have a random tessellation by dominoes.
2. Another way to generate a random tiling with dominoes is to set up all dominoes facing the same direction, then randomly select a neighboring pair to rotate by 90°:
   
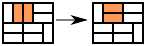
   Lay eight dominoes (or strips) on the domino rotation grid, and use random numbers (generate at random.org) to select pairs of dominoes to rotate by 90°. Perform about 20 rotations to produce a random tiling by dominoes.
3. Run this applet: Random Square Tiling a couple of times to produce random tilings of a square, and compare with your hand-made results.
4. This plus-shaped region is a simple example of a shape called an Aztec diamond.
   Draw all eight possible ways to tile the region with dominoes.
5. If you pick one of the eight tilings from question 4 at random, what is the probability that the top two squares are covered by a single domino, as in this picture:
6. This applet uses random pair rotations to produce a Random tiling of an Aztec Diamond. Does it seem likely that the top two squares will be covered by a single horizontal domino?
7. Try other similar applets here: Tiling Applets
8. Experiment with Paul Harrison's Ghost Diagrams Applet for many interesting random tilings.

Handin: A sheet with answers to all questions.