Aperiodic Tessellations

Relevant examples from Escher's work:
Non-periodic Tessellations
The tessellations covered to this point have all been periodic tessellations. They have translation symmetry, and so they look the same at different points in the plane. Periodic tessellations form patterns with symmetry given by one of the seventeen wallpaper groups.
A non-periodic tessellation is a tessellation which is not periodic. That is, a tessellation which has no translation symmetry. Escher's free form prints Mosaic and Mosaic II are examples of non-periodic tessellations, but they only cover a portion of the plane. Escher could certainly have extended these to cover more of the plane, but he would have had many decisions to make in order to continue. It is not hard to imagine a tessellation of the entire plane consisting of tiles which are all different. However, most of the mathematical interest in non-periodic tessellations comes from the search for examples that use a limited number of tiles.
Explorations
Begin learning about non-periodic tessellations with these:
Random Tessellations
An easy method for creating a non-periodic tiling using only one type of tile is to use triangles to make squares in two different ways. For example:
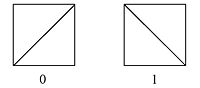
We label the squares with “0” and “1”. A random number generator (or a coin flip) can generate a string of 0’s and 1’s, which translate into squares that result in a tessellation with no translation symmetry. As an example, 64 random numbers were used to generate the following portion of an aperiodic tessellation:

Radial and Spiral Tilings
Another way to create beautiful non-periodic tilings is to choose tiles which can form concentric rings. The 30°-75°-75° isoceles triangle is one example, and it can form a radial tiling as shown below. By shifting the upper half of the radial tiling one triangle to the right, a spiral tiling is formed.
| A radial tiling | A spiral tiling |
|---|---|
 |

|
Substitution Tilings
A tile which can dissected into smaller copies of itself is called a rep-tile. A square is a rep-tile, since it can be cut into four smaller squares. Any parallelogram is a rep-tile, and so is any triangle. Here are some more interesting rep-tiles:
| The L | The Half-Hexagon | The Sphinx | The Pinwheel |
|---|---|---|---|
 |
 |
 |

|
A substitution tiling is created by a two-step process known as inflation. The first step of inflation is to enlarge an existing tile (or tessellation). The second step is to dissect each large tile into smaller tiles which are the same size and shape as the tiles of the original tessellation. Here is an example in which each larger square is cut into four smaller squares at each dissection step:

The inflation process produces larger and larger patches of tiles. One might expect than any tile which can cover large patches of the plane could actually cover the whole plane, but this is not a simple fact. It is known as the Extension Theorem[1]:
- The Extension Theorem
- Any reasonable set of tiles which can cover larger and larger patches must actually be able to cover the entire infinite plane.
The Extension Theorem is difficult to prove, and even giving a precise meaning of the term 'reasonable' requires advanced mathematics.
One consequence of the Extension Theorem is that substitution tilings actually work: any tile which can be cut into smaller copies of itself can be used to tessellate the plane.
Interesting rep-tiles can be used to make substitution tilings which are not periodic. For example, here are the first few inflations of the Sphinx substitution tiling:

To draw a substitution tiling by hand, begin with a large version of the tile, subdivide it into smaller copies of itself, and then continue subdividing each smaller copy until the desired level of detail is reached:

In the Extension Theorem, the tile (or tiles) are required to cover 'larger and larger' patches of the plane. This is intended to mean that the tile can cover as large a patch as desired, or that there is no limit to the size of a patch covered by the tile. One might ask if there is some patch size that is always large enough. As an example for thought, the tile shown below is a hexagon with one flat side, two spiked sides, and three dents. The spikes fit into the dents, and for a while this tile can build a tessellation, but eventually the dents outnumber the spikes and one gets stuck - Amman's dented hexagon cannot tile the plane, even though it can tile a fairly large patch:

This question of whether some patch size is large enough to force a tile to tessellate the entire plane is known as Heesch's problem, and is still unsolved. Casey Mann has an excellent page that states the question precisely and has many pictures of examples.
Penrose Tilings
The random, spiral, and rep-tile tessellations are not periodic, because they have no translation symmetry. However, they are all made from tiles which can easily be rearranged to form periodic tessellations. In the early 1960's, mathematicians began to search for a tile, or set of tiles, that can only form non-periodic tessellations. Such tiles are called aperiodic tiles:
- Aperiodic Tiles
- A set of tiles which can only tile the plane in a non-periodic manner.
Tessellations formed by aperiodic tiles are called aperiodic tessellations.
The first sets of aperiodic tiles were discovered by Roger Penrose, (who later became SIR Roger Penrose). Penrose, between 1972 and 1978, developed three sets of tiles that can only form aperiodic tessellations. The most famous set consists of two tiles, the kite and dart.
Both kite and dart are based on quadrilaterals with two long edges and two short edges, and additional small protrusions that force the edges to line up in a specific manner. The long edges are times as long as the short edges, where is the Golden Ratio. The angles are as shown below, all are multiples of 36°, and notice that 144° is the corner angle of a regular decagon (10 sides). The bumps on the edges are different shapes on the long and short sides, which force long sides to match with long sides, and short to match with short. The bumps are not centered on their respective sides, which restricts the matchings even more.
| Kite and Dart with bumps | Kite and Dart with markings |
|---|---|
 |
|
Because the bumps make the tiles more difficult to cut out or draw, the tiles are usually presented without the bumps. Instead, there are markings on the tile that are required to line up. The marked tiles fit together in a manner equivalent to the dented tiles, and also give rise to appealing patterns on any correct tessellation.
| A Penrose kite and dart tiling |
|---|

|
The bumps or markings rule out many possible arrangements of tiles. For example, these three configurations are illegal because the markings fail to line up:

|
In fact, with the dents (or markings) the two tiles can no longer form periodic tessellations.
To understand Penrose tilings, it is helpful to make some small tessellations by hand. Print out sheets of kite and dart tiles, cut them out, and then try to tessellate with them. You may find that after fitting together a handful of tiles, you become stuck and need to backtrack, removing tiles that seemed to fit but eventually made it impossible to continue.
Because the kite and dart tiles cannot form periodic tessellations, it is not even clear they tessellate at all. However, there is a substitution method that produces larger and larger patches of tessellation using an inflation process similar to the rep-tile examples . The Extension Theorem then implies that the Penrose tiles can tesselate the entire plane.

Despite their complicated mathematical nature, certain crystals that occur in nature share many properties with Penrose tilings. The first of these quasicrystals was discovered by Dan Shechtman in 1982, and his development of the field led to his Nobel Prize in Chemistry in 2011. Like Penrose tilings, these quasicrystals have regular structure but do not repeat periodically. Shechtman's discovery began when he created an Aluminum-Manganese alloy which exhibited order five rotational symmetry, which is not possible in any of the wallpaper groups (or their extensions into three dimensions).
One Aperiodic Tile?

The Penrose tiles are an aperiodic set of two tiles. Their discovery in the early 1970's raised the question:
Is there an aperiodic tile?
That is, is there a single tile which can tessellate the plane, but only in a non-periodic fashion?
In 2010, Joan Taylor of Tasmania came very close with the discovery of a hexagonal tile with markings that can only tile non-periodically[2]. The black bands must connect across tiles, and the purple swoops must match position and direction across each edge as well. The situation is especially complicated because the tile is allowed to flip over and the markings must be visible from both sides.

For Penrose tiles, the markings are just a simple way to indicate where bumps on the tile should be. However, no one was able to change the markings on Taylor's hexagon into dents or bumps. So the marked hexagon tile is very close to being a single aperiodic tile, but falls just short.
2023 update: Amateur mathematician David Smith discovered the "hat" tile, which does tessellate but can only do so aperiodically, solving this fifty year old problem.
Exercises
Aperiodic Tessellation Exercises
Related Sites
- wikipedia:Aperiodic tiling
- Aperiodic tilings, by Steven Dutch. With links to Radial, spiral, and Penrose tilings.
- The Tilings Encyclopedia, by E. Harriss and D. Frettlöh. Many aperiodic tilings.
- The Penrose tile in architecture
- Rep-tiles by Stewart Hinsley.
Notes
- ↑ Grunbaum, Shephard, Tilings and Patterns, 1987, Chapter 3.8
- ↑ Joshua Socolar, Joan Taylor, An aperiodic hexagonal tile, 2010, http://arxiv.org/pdf/1003.4279v2


